pacman::p_load(sf, sfdep, tmap, tidyverse)In-Class Exercise 5
In this exercise, we will perform global and local measures of spatial autocorrelation using sfdep package.
1 Exercise Reference
2 Overview
In this exercise, we will use the sfdep package to perform global and local measures of spatial autocorrelation using Hunan’s spatial data. In Hands-on Exercise 5, we learnt to perform spatial autocorrelation using spdep package.
The sfdep and spdep packages in R are both designed for spatial data analysis, particularly focusing on spatial autocorrelation, but they differ in their approach and compatibility with modern R data structures.
-
spdep: This is the older and more established package for spatial dependence analysis in R. It provides functions for creating spatial weights, spatial lag models, and global and local spatial autocorrelation statistics such as Moran’s I. However, spdep was originally built to work with the
sppackage, which uses the olderSpatial*classes for handling spatial data. -
sfdep: This is a newer package designed to work seamlessly with the sf package, which has become the standard for handling spatial data in R using simple features. sfdep provides an interface for spatial dependence analysis that is compatible with sf’s
sfobjects (simple feature geometries) and makes extensive use of tidyverse conventions, such as list columns, which allow for more flexible and tidy manipulation of spatial data.
2.1 Key Differences:
-
Data Structures:
-
spdep works with
Spatial*objects from thesppackage. -
sfdep works with
sfobjects from thesfpackage, which are easier to integrate with modern R workflows and the tidyverse ecosystem.
-
spdep works with
-
Integration:
- sfdep is more compatible with modern workflows using the tidyverse, allowing for easier manipulation of data within data frames and list columns.
- spdep relies on the older base R style and is less intuitive when working with modern data pipelines.
-
Functionality:
- Both packages provide similar functionalities for spatial autocorrelation, such as computing Moran’s I and local Moran’s I.
- sfdep introduces new functionalities that leverage list columns for easier spatial dependence operations.
sfdep can essentially be considered a wrapper around the functionality provided by spdep, designed to work with the modern sf (simple features) framework for spatial data in R.
3 Learning Outcome
- Perform global Moran’s I test for spatial autocorrelation.
- Compute and visualize local Moran’s I and Gi* statistics for identifying clusters and outliers.
- Create choropleth maps to display the results of spatial autocorrelation analysis.
4 Import the R Packages
The following R packages will be used in this exercise:
| Package | Purpose | Use Case in Exercise |
|---|---|---|
| sf | Handles spatial data; imports, manages, and processes vector-based geospatial data. | Importing and managing geospatial data, such as Hunan’s county boundary shapefile. |
| sfdep | Provides functions for spatial autocorrelation, including Moran’s I and local Moran’s I. | Performing spatial autocorrelation analysis with global and local measures. |
| tidyverse | A collection of R packages for data science tasks like data manipulation, visualization, and modeling. | Wrangling aspatial data and joining with spatial datasets. |
| tmap | Creates static and interactive thematic maps using cartographic quality elements. | Visualizing spatial analysis results and creating thematic maps. |
To install and load these packages, use the following code:
5 The Data
The following datasets will be used in this exercise:
| Data Set | Description | Format |
|---|---|---|
| Hunan County Boundary Layer | A geospatial dataset containing Hunan’s county boundaries. | ESRI Shapefile |
| Hunan_2012.csv | A CSV file containing selected local development indicators for Hunan in 2012. | CSV |
hunan <- st_read(dsn = "data/geospatial",
layer = "Hunan")Reading layer `Hunan' from data source
`/Users/walter/code/isss626/isss626-gaa/In-class_Ex/In-class_Ex05/data/geospatial'
using driver `ESRI Shapefile'
Simple feature collection with 88 features and 7 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS: WGS 84glimpse(hunan)Rows: 88
Columns: 8
$ NAME_2 <chr> "Changde", "Changde", "Changde", "Changde", "Changde", "Cha…
$ ID_3 <int> 21098, 21100, 21101, 21102, 21103, 21104, 21109, 21110, 211…
$ NAME_3 <chr> "Anxiang", "Hanshou", "Jinshi", "Li", "Linli", "Shimen", "L…
$ ENGTYPE_3 <chr> "County", "County", "County City", "County", "County", "Cou…
$ Shape_Leng <dbl> 1.869074, 2.360691, 1.425620, 3.474325, 2.289506, 4.171918,…
$ Shape_Area <dbl> 0.10056190, 0.19978745, 0.05302413, 0.18908121, 0.11450357,…
$ County <chr> "Anxiang", "Hanshou", "Jinshi", "Li", "Linli", "Shimen", "L…
$ geometry <POLYGON [°]> POLYGON ((112.0625 29.75523..., POLYGON ((112.2288 …For admin boundaries, we will typically encounter polygon or multipolygon data objects.
A polygon represents a single contiguous area, while a multipolygon consists of multiple disjoint areas grouped together (e.g., islands that belong to the same admin region).
hunan2012 <- read_csv("data/aspatial/Hunan_2012.csv")
glimpse(hunan2012)Rows: 88
Columns: 29
$ County <chr> "Anhua", "Anren", "Anxiang", "Baojing", "Chaling", "Changn…
$ City <chr> "Yiyang", "Chenzhou", "Changde", "Hunan West", "Zhuzhou", …
$ avg_wage <dbl> 30544, 28058, 31935, 30843, 31251, 28518, 54540, 28597, 33…
$ deposite <dbl> 10967.0, 4598.9, 5517.2, 2250.0, 8241.4, 10860.0, 24332.0,…
$ FAI <dbl> 6831.7, 6386.1, 3541.0, 1005.4, 6508.4, 7920.0, 33624.0, 1…
$ Gov_Rev <dbl> 456.72, 220.57, 243.64, 192.59, 620.19, 769.86, 5350.00, 1…
$ Gov_Exp <dbl> 2703.0, 1454.7, 1779.5, 1379.1, 1947.0, 2631.6, 7885.5, 11…
$ GDP <dbl> 13225.0, 4941.2, 12482.0, 4087.9, 11585.0, 19886.0, 88009.…
$ GDPPC <dbl> 14567, 12761, 23667, 14563, 20078, 24418, 88656, 10132, 17…
$ GIO <dbl> 9276.90, 4189.20, 5108.90, 3623.50, 9157.70, 37392.00, 513…
$ Loan <dbl> 3954.90, 2555.30, 2806.90, 1253.70, 4287.40, 4242.80, 4053…
$ NIPCR <dbl> 3528.3, 3271.8, 7693.7, 4191.3, 3887.7, 9528.0, 17070.0, 3…
$ Bed <dbl> 2718, 970, 1931, 927, 1449, 3605, 3310, 582, 2170, 2179, 1…
$ Emp <dbl> 494.310, 290.820, 336.390, 195.170, 330.290, 548.610, 670.…
$ EmpR <dbl> 441.4, 255.4, 270.5, 145.6, 299.0, 415.1, 452.0, 127.6, 21…
$ EmpRT <dbl> 338.0, 99.4, 205.9, 116.4, 154.0, 273.7, 219.4, 94.4, 174.…
$ Pri_Stu <dbl> 54.175, 33.171, 19.584, 19.249, 33.906, 81.831, 59.151, 18…
$ Sec_Stu <dbl> 32.830, 17.505, 17.819, 11.831, 20.548, 44.485, 39.685, 7.…
$ Household <dbl> 290.4, 104.6, 148.1, 73.2, 148.7, 211.2, 300.3, 76.1, 139.…
$ Household_R <dbl> 234.5, 121.9, 135.4, 69.9, 139.4, 211.7, 248.4, 59.6, 110.…
$ NOIP <dbl> 101, 34, 53, 18, 106, 115, 214, 17, 55, 70, 44, 84, 74, 17…
$ Pop_R <dbl> 670.3, 243.2, 346.0, 184.1, 301.6, 448.2, 475.1, 189.6, 31…
$ RSCG <dbl> 5760.60, 2386.40, 3957.90, 768.04, 4009.50, 5220.40, 22604…
$ Pop_T <dbl> 910.8, 388.7, 528.3, 281.3, 578.4, 816.3, 998.6, 256.7, 45…
$ Agri <dbl> 4942.253, 2357.764, 4524.410, 1118.561, 3793.550, 6430.782…
$ Service <dbl> 5414.5, 3814.1, 14100.0, 541.8, 5444.0, 13074.6, 17726.6, …
$ Disp_Inc <dbl> 12373, 16072, 16610, 13455, 20461, 20868, 183252, 12379, 1…
$ RORP <dbl> 0.7359464, 0.6256753, 0.6549309, 0.6544614, 0.5214385, 0.5…
$ ROREmp <dbl> 0.8929619, 0.8782065, 0.8041262, 0.7460163, 0.9052651, 0.7…Recall that to do left join, we need a common identifier between the 2 data objects. The content must be the same eg. same format and same case. In Hands-on Exercise 1B, we need to (PA, SZ) in the dataset to uppercase before we can join the data.
hunan <- left_join(hunan,hunan2012) %>%
select(1:4, 7, 15)
glimpse(hunan)Rows: 88
Columns: 7
$ NAME_2 <chr> "Changde", "Changde", "Changde", "Changde", "Changde", "Chan…
$ ID_3 <int> 21098, 21100, 21101, 21102, 21103, 21104, 21109, 21110, 2111…
$ NAME_3 <chr> "Anxiang", "Hanshou", "Jinshi", "Li", "Linli", "Shimen", "Li…
$ ENGTYPE_3 <chr> "County", "County", "County City", "County", "County", "Coun…
$ County <chr> "Anxiang", "Hanshou", "Jinshi", "Li", "Linli", "Shimen", "Li…
$ GDPPC <dbl> 23667, 20981, 34592, 24473, 25554, 27137, 63118, 62202, 7066…
$ geometry <POLYGON [°]> POLYGON ((112.0625 29.75523..., POLYGON ((112.2288 2…6 Visualising Choropleth Map of GDPPC of Hunan
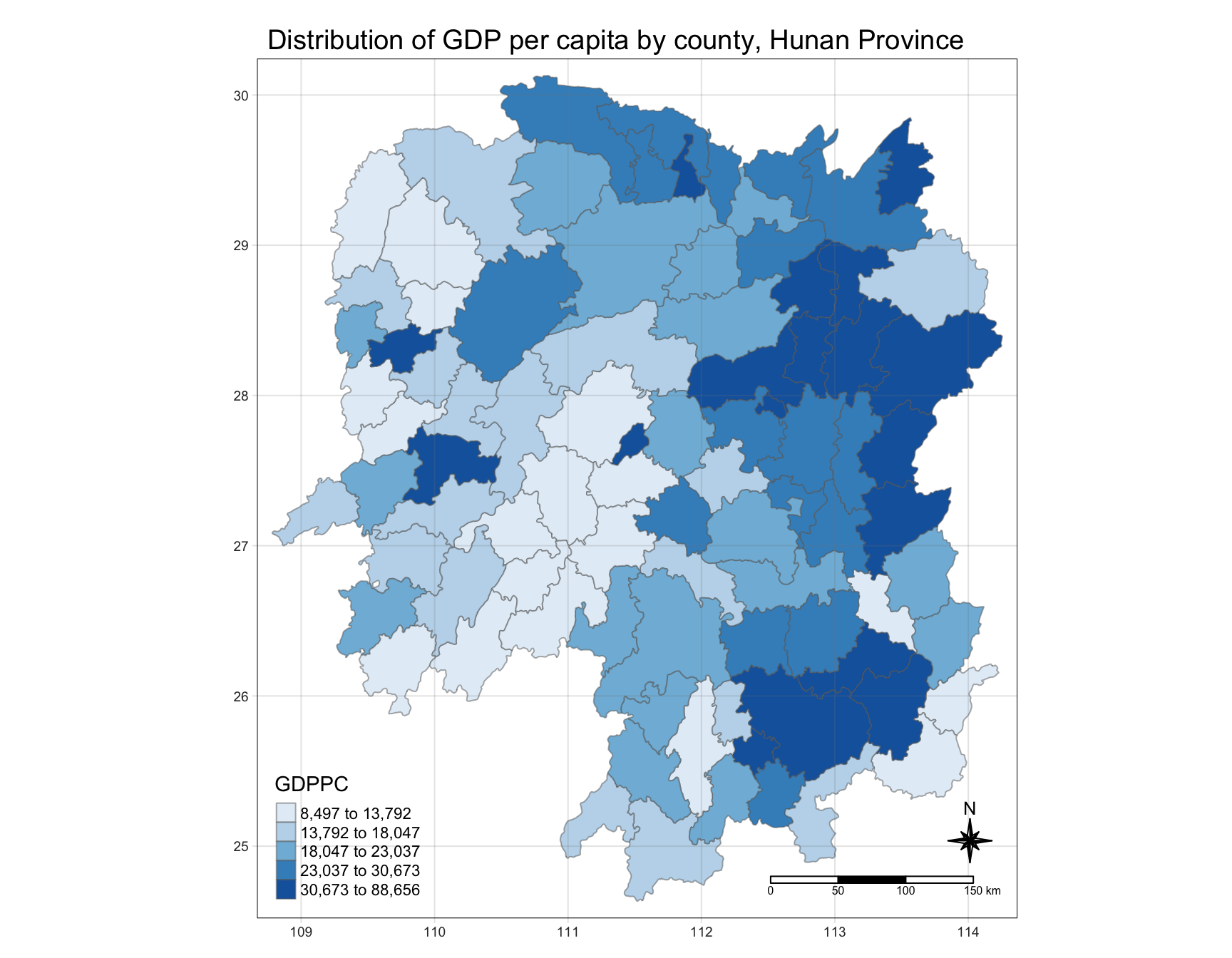
To plot a choropleth map showing the distribution of GDPPC of Hunan province:
tmap_mode("plot")
tm_shape(hunan) +
tm_fill("GDPPC",
style = "quantile",
palette = "Blues",
title = "GDPPC") +
tm_layout(main.title = "Distribution of GDP per capita by county, Hunan Province",
main.title.position = "center",
main.title.size = 1.2,
legend.height = 0.45,
legend.width = 0.35,
frame = TRUE) +
tm_borders(alpha = 0.5) +
tm_compass(type="8star", size = 2) +
tm_scale_bar() +
tm_grid(alpha =0.2)
7 Global Measures of Spatial Association
7.1 Deriving Queen’s contiguity weights: sfdep methods
To derive the Queen’s contiguity weights:
wm_q <- hunan %>%
mutate(nb = st_contiguity(geometry),
wt = st_weights(nb,
style = "W"),
.before = 1)
Notice that st_weights() provides tree arguments,
they are:
- nb: A neighbor list object as created by st_neighbors().
- style: Default “W” for row standardized weights. This value can also be “B”, “C”, “U”, “minmax”, and “S”. B is the basic binary coding, W is row standardised (sums over all links to n), C is globally standardised (sums over all links to n), U is equal to C divided by the number of neighbours (sums over all links to unity), while S is the variance-stabilizing coding scheme proposed by Tiefelsdorf et al. 1999, p. 167-168 (sums over all links to n).
- allow_zero: If TRUE, assigns zero as lagged value to zone without neighbors.
7.2 Computing Global Moran’ I
We will use
global_moran()
function to compute the Moran’s I value.
moranI <- global_moran(
wm_q$GDPPC, # Target variable: GDP per capita
wm_q$nb, # Neighborhood structure
wm_q$wt # Spatial weights
)
glimpse(moranI)List of 2
$ I: num 0.301
$ K: num 7.64
Unlike the spdep package, the output of the
global_moran() function is a tibble data frame,
making it easier to work with in the tidyverse environment.
8 Performing Global Moran’s I Test
Previously, we calculated the Moran’s I statistic using the
global_moran() function. However, this approach
does not allow for formal hypothesis testing, as it only returns
the Moran’s I value, not the associated p-value or significance
level. Therefore, we cannot determine whether spatial
autocorrelation is statistically significant with this method.
To conduct a proper hypothesis test, we need to use the
global_moran_test() function from the
sfdep package, which computes the Moran’s I statistic
and also performs a permutation-based significance test. This allows
us to assess whether the observed spatial autocorrelation is
significantly different from what would be expected under spatial
randomness.
The following code demonstrates how to perform the Moran’s I test:
global_moran_test(
wm_q$GDPPC, # Target variable: GDP per capita
wm_q$nb, # Neighborhood structure
wm_q$wt # Spatial weights
)
Moran I test under randomisation
data: x
weights: listw
Moran I statistic standard deviate = 4.7351, p-value = 1.095e-06
alternative hypothesis: greater
sample estimates:
Moran I statistic Expectation Variance
0.300749970 -0.011494253 0.004348351 -
The default for
alternativeargument is “two.sided”. Other supported arguments are “greater” or “less”. randomization, and -
By default the
randomizationargument is TRUE. If FALSE, under the assumption of normality.
This method not only calculates the Moran’s I statistic but also provides a p-value for assessing the significance of the spatial autocorrelation.
Observations:
- Moran’s I statistic: 0.301, indicating moderate positive spatial autocorrelation.
- P-value: 1.095e-06, highly significant, confirming strong evidence of positive spatial autocorrelation.
9 Perfoming Global Moran’s I Permutation Test
In practice, a Monte Carlo simulation should be used to perform the
statistical test. In the sfdep package, this is
supported by the global_moran_perm() function.
To ensure that the computation is reproducible, we will use
set.seed()
before performing simulation.
set.seed(1234)
Now we will perform Monte Carlo simulation using
global_moran_perm().
global_moran_perm(wm_q$GDPPC,
wm_q$nb,
wm_q$wt,
nsim = 99)
Monte-Carlo simulation of Moran I
data: x
weights: listw
number of simulations + 1: 100
statistic = 0.30075, observed rank = 100, p-value < 2.2e-16
alternative hypothesis: two.sidedObservations:
The statistical report on previous tab shows that the p-value is smaller than alpha value of 0.05. Hence, we have enough statistical evidence to reject the null hypothesis that the spatial distribution of GPD per capita are resemble random distribution (i.e. independent from spatial). Because the Moran’s I statistics is greater than 0. We can infer that the spatial distribution shows sign of clustering.
10 Local Measures of Spatial Association
11 LISA Map
LISA map is a categorical map showing outliers and clusters. There are two types of outliers namely: High-Low and Low-High outliers. Likewise, there are two type of clusters namely: High-High and Low-Low cluaters. In fact, LISA map is an interpreted map by combining local Moran’s I of geographical areas and their respective p-values.
12 Computing Local Moran’s I
In this section, we will compute Local Moran’s I of GDPPC at county
level by using
local_moran()
of sfdep package.
lisa <- wm_q %>%
mutate(local_moran = local_moran(
GDPPC, nb, wt, nsim = 99),
.before = 1) %>%
unnest(local_moran)-
We use
unnest()in this context to convert the nested list column created bylocal_moran()into multiple rows, one for each simulation result per observation. -
The
local_moran()function from thesfdeppackage returns a nested list, with each element containing the results of local Moran’s I statistic for each spatial unit. - Unnesting helps in expanding this list into individual rows, making each result (e.g., local Moran’s I values, p-values) accessible in a tidy, flat data frame format.
- This step is crucial for easier manipulation, filtering, and visualization of the spatial autocorrelation results, allowing us to work with the data in a more intuitive and flexible way.
Thus, unnest() is applied to handle and process the
simulation results efficiently.
The output of local_moran() is a sf data.frame
containing the columns ii, eii, var_ii, z_ii, p_ii, p_ii_sim,
and p_folded_sim.
- ii: local moran statistic
- eii: expectation of local moran statistic; for localmoran_permthe permutation sample means
- var_ii: variance of local moran statistic; for localmoran_permthe permutation sample standard deviations
-
z_ii: standard deviate of local moran statistic; for
localmoran_perm based on permutation sample means and standard
deviations p_ii: p-value of local moran statistic using
pnorm(); for localmoran_perm using standard deviatse based on
permutation sample means and standard deviations p_ii_sim: For
localmoran_perm(),rank()andpunif()of observed statistic rank for [0, 1] p-values usingalternative=-p_folded_sim: the simulation folded [0, 0.5] range ranked p-value (based on https://github.com/pysal/esda/blob/4a63e0b5df1e754b17b5f1205b cadcbecc5e061/esda/crand.py#L211-L213) -
skewness: For
localmoran_perm, the output of e1071::skewness() for the permutation samples underlying the standard deviates -
kurtosis: For
localmoran_perm, the output of e1071::kurtosis() for the permutation samples underlying the standard deviates.
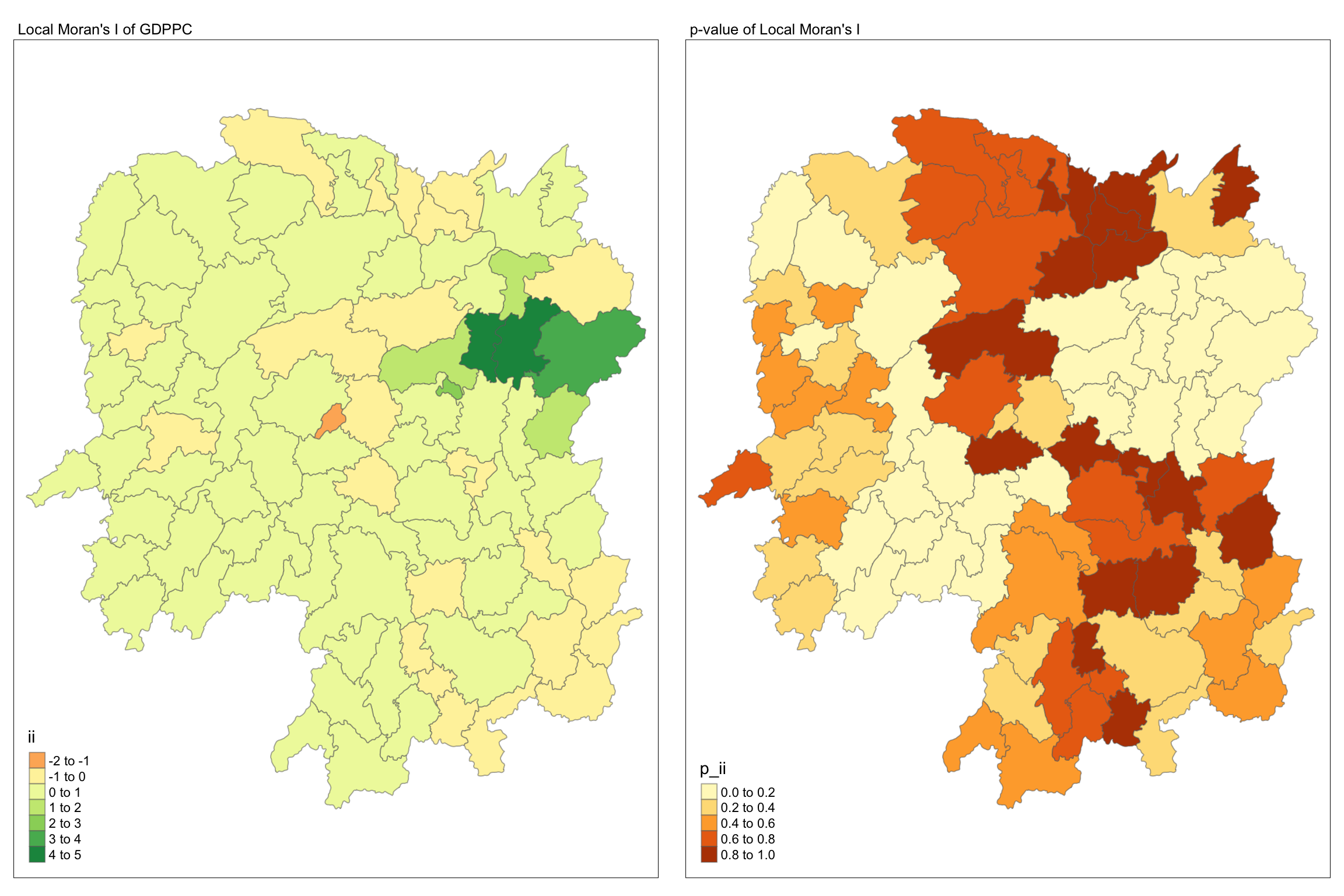
13 Visualising Local Moran’s I and p-value
When interpreting / visualizing local Moran’s I, we should plot the Moran’s I and p-value side by side.
tmap_mode("plot")
map1 <- tm_shape(lisa) +
tm_fill("ii") +
tm_borders(alpha = 0.5) +
tm_view(set.zoom.limits = c(6,8)) +
tm_layout(
main.title = "Local Moran's I of GDPPC",
main.title.size = 0.8
)
map2 <- tm_shape(lisa) +
tm_fill("p_ii") +
tm_borders(alpha = 0.5) +
tm_view(set.zoom.limits = c(6,8)) +
tm_layout(
main.title = "p-value of Local Moran's I",
main.title.size = 0.8
)
tmap_arrange(map1, map2, ncol = 2)
13.1 Plotting LISA Map
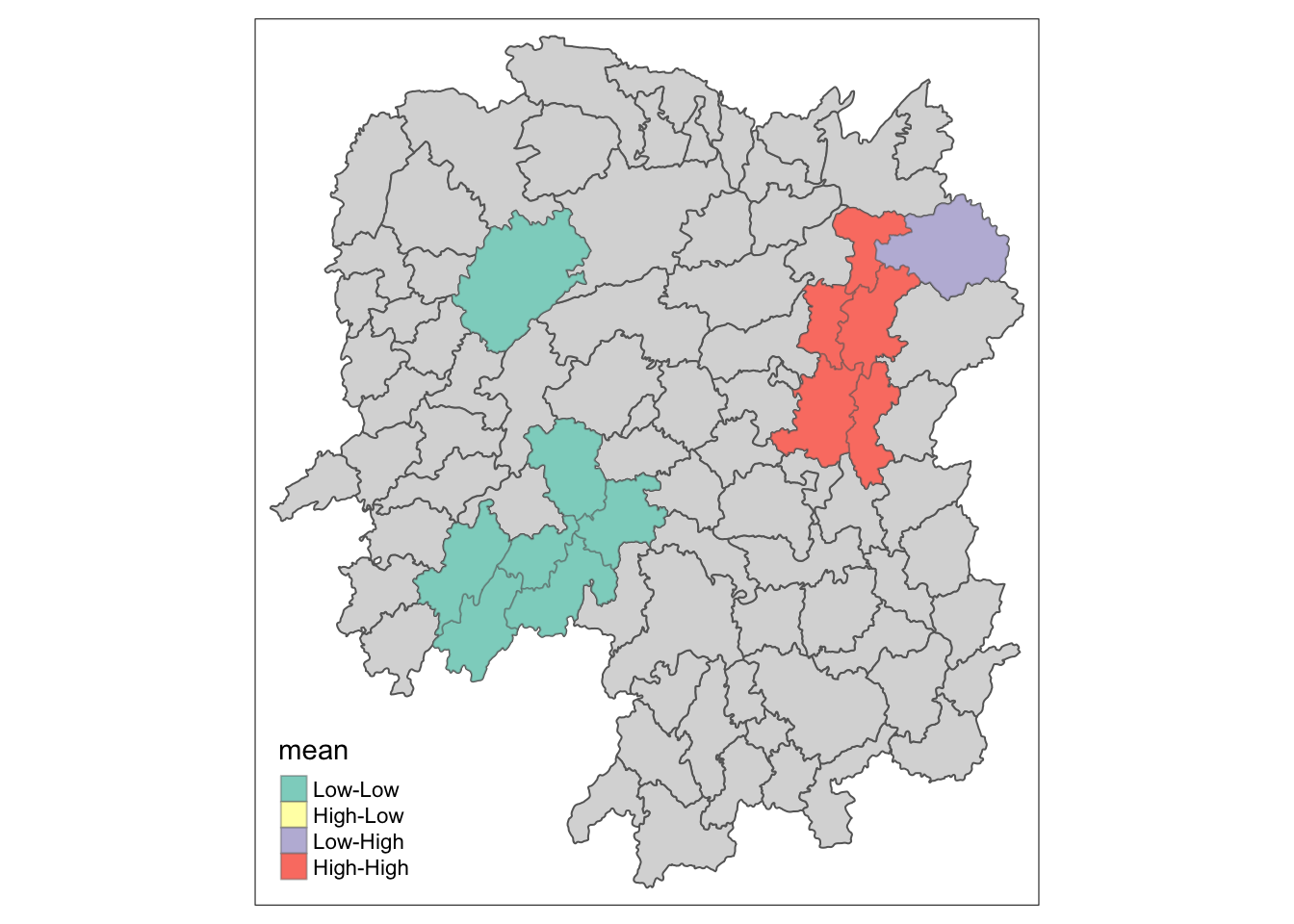
In lisa sf data.frame, we can find three fields contain the LISA categories. They are mean, median and pysal. In general, classification in mean will be used as shown in the code below.
lisa_sig <- lisa %>%
filter(p_ii_sim < 0.05)
tmap_mode("plot")
tm_shape(lisa) +
tm_polygons() +
tm_borders(alpha = 0.5) +
tm_shape(lisa_sig) +
tm_fill("mean") +
tm_borders(alpha = 0.4)
14 Hot Spot and Cold Spot Area Analysis
Hot Spot and Cold Spot Analysis (HCSA) uses spatial weights to identify locations of statistically significant hot spots and cold spots within a spatially weighted attribute. These spots are identified based on a calculated distance that groups features when similar high (hot) or low (cold) values are found in proximity to one another. The polygon features typically represent administrative boundaries or a custom grid structure.
14.1 Computing local Gi* statistics
As usual, we will need to derive a spatial weight matrix before we can compute local Gi* statistics. Code chunk below will be used to derive a spatial weight matrix by using sfdep functions and tidyverse approach.
wm_idw <- hunan %>%
mutate(nb = include_self(
st_contiguity(geometry)),
wts = st_inverse_distance(nb,
geometry,
scale = 1,
alpha = 1),
.before = 1)- Gi* and local Gi* are distance-based spatial statistics. Hence, distance methods instead of contiguity methods should be used to derive the spatial weight matrix.
-
Since we are going to compute Gi* statistics,
include_self()is used.
14.2 Computing Local Gi* statistics
Now, we will compute the local Gi* by using the code below.
HCSA <- wm_idw %>%
mutate(local_Gi = local_gstar_perm(
GDPPC, nb, wts, nsim = 99),
.before = 1) %>%
unnest(local_Gi)
HCSASimple feature collection with 88 features and 18 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS: WGS 84
# A tibble: 88 × 19
gi_star cluster e_gi var_gi std_dev p_value p_sim p_folded_sim skewness
<dbl> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.261 Low 0.00126 1.07e-7 0.283 7.78e-1 0.66 0.33 0.783
2 -0.276 Low 0.000969 4.76e-8 -0.123 9.02e-1 0.98 0.49 0.713
3 0.00573 High 0.00156 2.53e-7 -0.0571 9.54e-1 0.78 0.39 0.972
4 0.528 High 0.00155 2.97e-7 0.321 7.48e-1 0.56 0.28 0.942
5 0.466 High 0.00137 2.76e-7 0.386 7.00e-1 0.52 0.26 1.32
6 -0.445 High 0.000992 7.08e-8 -0.588 5.57e-1 0.68 0.34 0.692
7 2.99 High 0.000700 4.05e-8 3.13 1.74e-3 0.04 0.02 0.975
8 2.04 High 0.00152 1.58e-7 1.77 7.59e-2 0.16 0.08 1.26
9 4.42 High 0.00130 1.18e-7 4.22 2.39e-5 0.02 0.01 1.20
10 1.21 Low 0.00175 1.25e-7 1.49 1.36e-1 0.18 0.09 0.408
# ℹ 78 more rows
# ℹ 10 more variables: kurtosis <dbl>, nb <nb>, wts <list>, NAME_2 <chr>,
# ID_3 <int>, NAME_3 <chr>, ENGTYPE_3 <chr>, County <chr>, GDPPC <dbl>,
# geometry <POLYGON [°]>14.3 Visualising Local Hot Spot and Cold Spot Areas (HCSA)
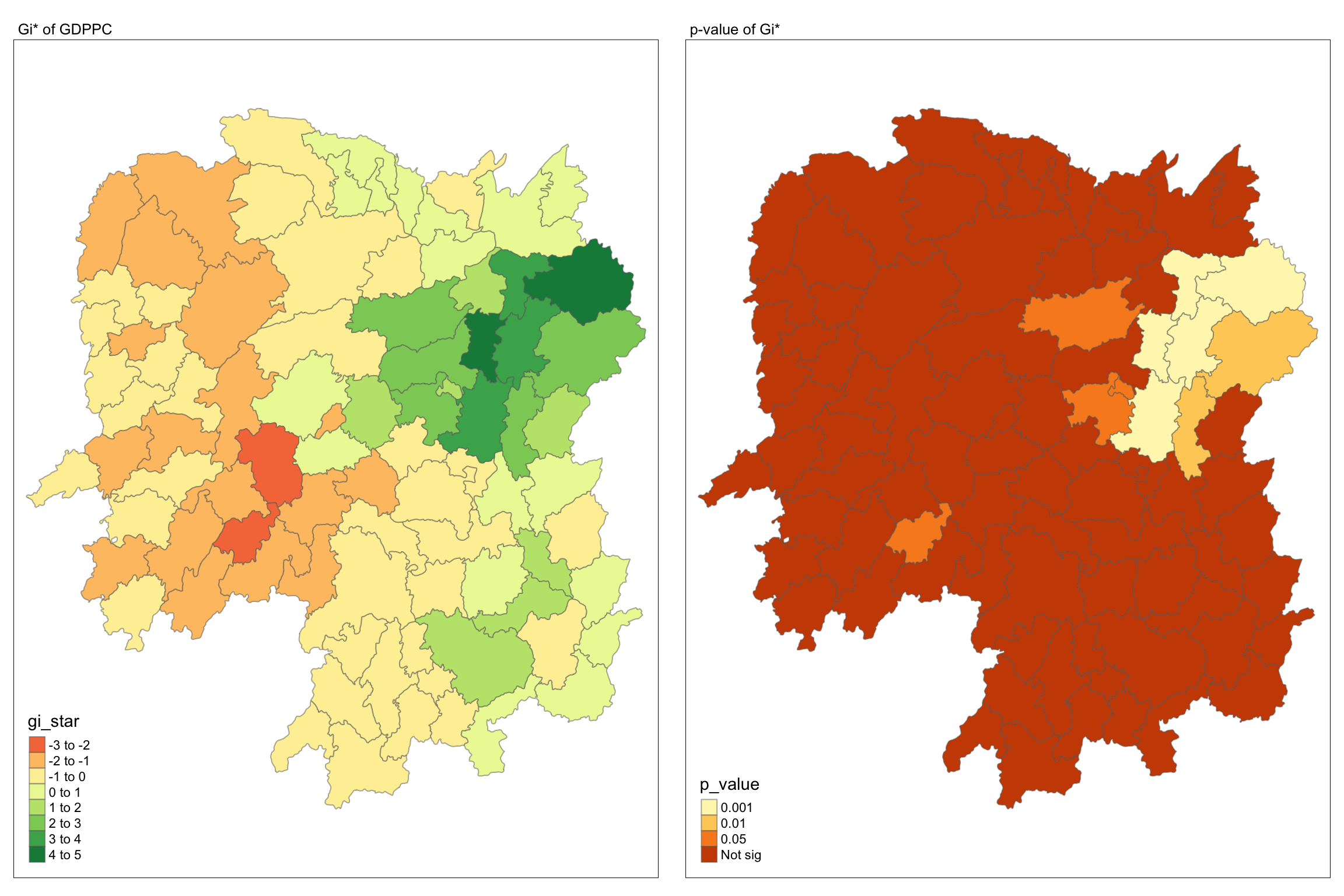
Similarly, for effective comparison, we should plot the local Gi* values with its p-value.
tmap_mode("plot")
map1 <- tm_shape(HCSA) +
tm_fill("gi_star") +
tm_borders(alpha = 0.5) +
tm_view(set.zoom.limits = c(6,8)) +
tm_layout(main.title = "Gi* of GDPPC",
main.title.size = 0.8)
map2 <- tm_shape(HCSA) +
tm_fill("p_value",
breaks = c(0, 0.001, 0.01, 0.05, 1),
labels = c("0.001", "0.01", "0.05", "Not sig")) +
tm_borders(alpha = 0.5) +
tm_layout(main.title = "p-value of Gi*",
main.title.size = 0.8)
tmap_arrange(map1, map2, ncol = 2)
To visualize HCSA, we will plot the significant (i.e. p-values less than 0.05) hot spot and cold spot areas by using appropriate tmap functions as shown below.
HCSA_sig <- HCSA %>%
filter(p_sim < 0.05)
tmap_mode("plot")
tm_shape(HCSA) +
tm_polygons() +
tm_borders(alpha = 0.5) +
tm_shape(HCSA_sig) +
tm_fill("cluster") +
tm_borders(alpha = 0.4)
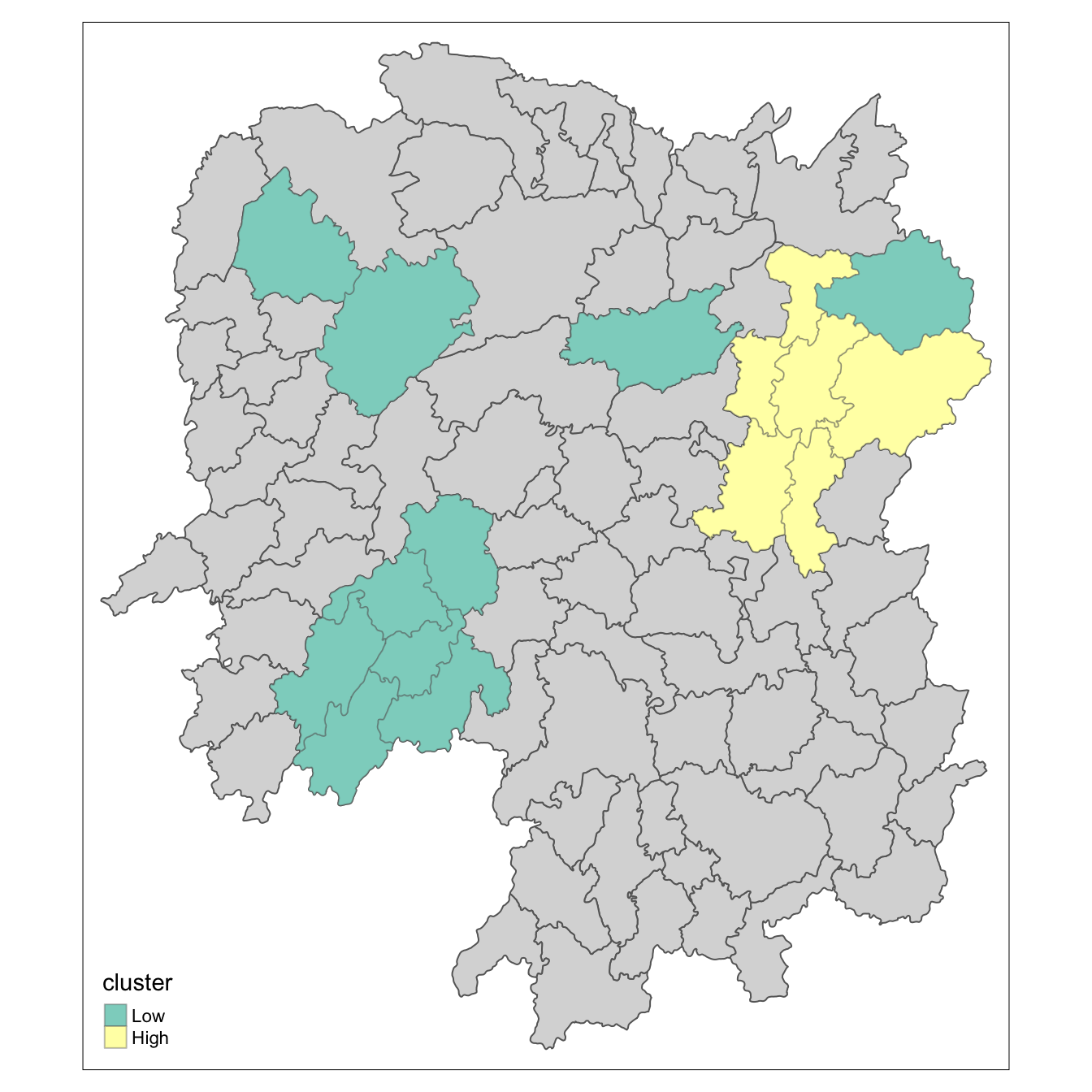
Observations: The plot reveals that there is one hot spot area and two cold spot areas. Interestingly, the hot spot areas coincide with the High-high cluster identifies by using local Moran’s I method in the earlier sub-section.