In-Class Exercise 2

In this exercise, we will learn to analyze spatial point patterns using spatstat methods, including installing necessary packages, creating spatial objects, performing kernel density estimation, and applying edge correction methods.

Author

Teng Kok Wai (Walter)

Published

September 2, 2024

Modified

September 27, 2024

1 Exercise Reference

ISSS626 Geospatial Analytics and Applications - In-class Exercise 2: Spatial Point Patterns Analysis: spatstat methods

2 Learning Outcome

  • Understand how to handle the retired R package such as maptools
  • Understand the difference in usage of st_combine() and st_union() in the sf package.
  • Recap on usage of the spatstat package for analyzing two-dimensional spatial point patterns.
  • Recap on conversion steps of sf data frames to ppp and owin objects using as.ppp() and as.owin() functions for point pattern analysis.
  • Recap on Kernel Density Estimation (KDE) on spatial point events and visualize results usingspatstat.geom methods.
  • Understand importance of setting random seed for reproducible results when applying Monte Carlo simulations for spatial analysis.
  • Practice importing and visualizing data from regional data sources in preparation for Take Home Assignment 1

3 How to Handle Retired R Packages

In our work, we might need to use retired R packages. In this section, we will see how we can use a retired package such as maptools.

Although maptools is retired and removed from CRAN, we can still download from Posit Public Package Manager snapshots by using the code block below.

Tip

Include #| eval: false in the installation code block to avoid repetitively downloads of maptools whenever the Quarto document is rendered. 

install.packages("maptools",
                 repos = "https://packagemanager.posit.co/cran/2023-10-13")

4 Understanding the Salient Differences Between st_combine() and st_union()

In sf package, there are two functions allow us to combine multiple simple features into one simple features. They are st_combine() and st_union().

Tip

  • st_combine() returns a single, combined geometry, with no resolved boundaries; returned geometries may well be invalid.

  • If y is missing, st_union(x) returns a single geometry with resolved boundaries, else the geometries for all unioned pairs of x[i] and y[j].

see Combine or union feature geometries — geos_combine • sf

5 Understanding the spatstat Package

spatstat R package is a comprehensive open-source toolbox for analysing Spatial Point Patterns. Focused mainly on two-dimensional point patterns, including multitype or marked points, in any spatial region.

It comprises of many sub-packages for specific usage.

Package Description
spatstat Contains documentation and introductory material, including beginner’s guides, vignettes, and demos.
spatstat.data Contains all datasets required for the spatstat package.
spatstat.utils Provides basic utility functions for use within spatstat.
spatstat.univar Contains functions for estimating and manipulating probability distributions of 1-dimensional random variables.
spatstat.sparse Functions for handling sparse arrays and performing linear algebra operations.
spatstat.geom Defines spatial objects (e.g., point patterns, windows, pixel images) and includes geometrical operations.
spatstat.random Functions for generating random spatial patterns and simulating models.
spatstat.explore Code for exploratory data analysis and nonparametric spatial data analysis.
spatstat.model Code for model-fitting, diagnostics, and formal inference within spatial data analysis.
spatstat.linnet Defines spatial data on linear networks and performs geometrical operations and statistical analysis.

6 Creating ppp Objects from sf data.frame

We can derive an ppp object layer directly from a sf tibble data.frame using as.ppp() from spatstat.geom. 

childcare_ppp <- as.ppp(childcare_sf)
plot(childcare_ppp)

summary(childcare_ppp)
Marked planar point pattern:  1545 points
Average intensity 1.91145e-06 points per square unit

Coordinates are given to 11 decimal places

marks are of type 'character'
Summary:
   Length     Class      Mode
     1545 character character

Window: rectangle = [11203.01, 45404.24] x [25667.6, 49300.88] units
                    (34200 x 23630 units)
Window area = 808287000 square units

From the output above, we can observe the properties of the ppp objects.

7 Creating owin object from sf data.frame

We can create owin object from polygon sf tibble data.frame using as.owin() of spatstat.geom. 

sg_owin <- as.owin(sg_sf)
plot(sg_owin)

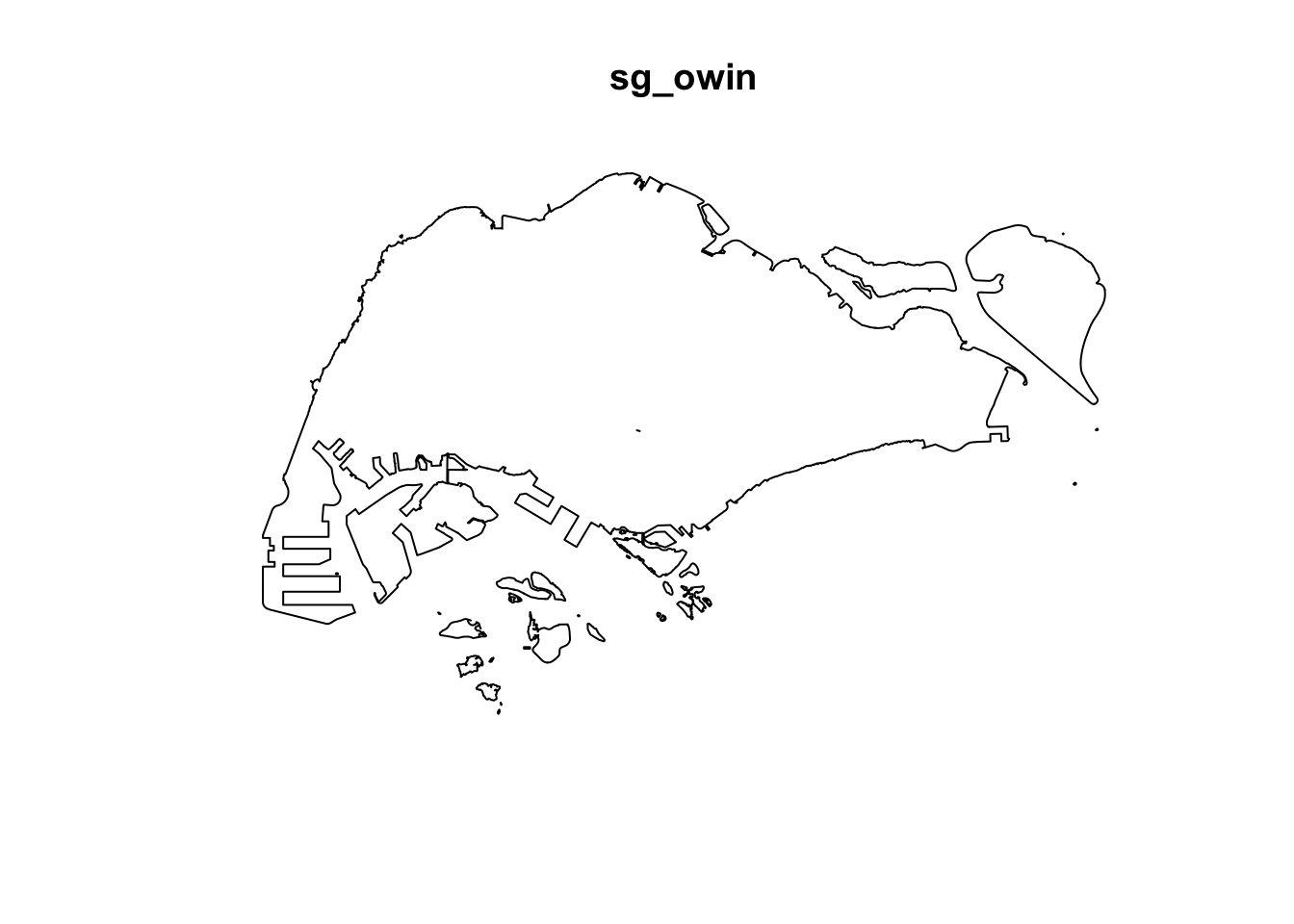
summary(sg_owin)
Window: polygonal boundary
80 separate polygons (35 holes)
                  vertices         area relative.area
polygon 1            14650  6.97996e+08      8.93e-01
polygon 2 (hole)         3 -2.21090e+00     -2.83e-09
polygon 3              285  1.61128e+06      2.06e-03
polygon 4 (hole)         3 -2.05920e-03     -2.63e-12
polygon 5 (hole)         3 -8.83647e-03     -1.13e-11
polygon 6              668  5.40368e+07      6.91e-02
polygon 7               44  2.26577e+03      2.90e-06
polygon 8               27  1.50315e+04      1.92e-05
polygon 9              711  1.28815e+07      1.65e-02
polygon 10 (hole)       36 -4.01660e+04     -5.14e-05
polygon 11 (hole)      317 -5.11280e+04     -6.54e-05
polygon 12 (hole)        3 -3.41405e-01     -4.37e-10
polygon 13 (hole)        3 -2.89050e-05     -3.70e-14
polygon 14              77  3.29939e+05      4.22e-04
polygon 15              30  2.80002e+04      3.58e-05
polygon 16 (hole)        3 -2.83151e-01     -3.62e-10
polygon 17              71  8.18750e+03      1.05e-05
polygon 18 (hole)        3 -1.68316e-04     -2.15e-13
polygon 19 (hole)       36 -7.79904e+03     -9.97e-06
polygon 20 (hole)        4 -2.05611e-02     -2.63e-11
polygon 21 (hole)        3 -2.18000e-06     -2.79e-15
polygon 22 (hole)        3 -3.65501e-03     -4.67e-12
polygon 23 (hole)        3 -4.95057e-02     -6.33e-11
polygon 24 (hole)        3 -3.99521e-02     -5.11e-11
polygon 25 (hole)        3 -6.62377e-01     -8.47e-10
polygon 26 (hole)        3 -2.09065e-03     -2.67e-12
polygon 27              91  1.49663e+04      1.91e-05
polygon 28 (hole)       26 -1.25665e+03     -1.61e-06
polygon 29 (hole)      349 -1.21433e+03     -1.55e-06
polygon 30 (hole)       20 -4.39069e+00     -5.62e-09
polygon 31 (hole)       48 -1.38338e+02     -1.77e-07
polygon 32 (hole)       28 -1.99862e+01     -2.56e-08
polygon 33              40  1.38607e+04      1.77e-05
polygon 34 (hole)       40 -6.00381e+03     -7.68e-06
polygon 35 (hole)        7 -1.40545e-01     -1.80e-10
polygon 36 (hole)       12 -8.36709e+01     -1.07e-07
polygon 37              45  2.51218e+03      3.21e-06
polygon 38             142  3.22293e+03      4.12e-06
polygon 39             148  3.10395e+03      3.97e-06
polygon 40              75  1.73526e+04      2.22e-05
polygon 41              83  5.28920e+03      6.76e-06
polygon 42             211  4.70521e+05      6.02e-04
polygon 43             106  3.04104e+03      3.89e-06
polygon 44             266  1.50631e+06      1.93e-03
polygon 45              71  5.63061e+03      7.20e-06
polygon 46              10  1.99717e+02      2.55e-07
polygon 47             478  2.06120e+06      2.64e-03
polygon 48             155  2.67502e+05      3.42e-04
polygon 49            1027  1.27782e+06      1.63e-03
polygon 50 (hole)        3 -1.16959e-03     -1.50e-12
polygon 51              65  8.42861e+04      1.08e-04
polygon 52              47  3.82087e+04      4.89e-05
polygon 53               6  4.50259e+02      5.76e-07
polygon 54             132  9.53357e+04      1.22e-04
polygon 55 (hole)        3 -3.23310e-04     -4.13e-13
polygon 56               4  2.69313e+02      3.44e-07
polygon 57 (hole)        3 -1.46474e-03     -1.87e-12
polygon 58            1045  4.44510e+06      5.68e-03
polygon 59              22  6.74651e+03      8.63e-06
polygon 60              64  3.43149e+04      4.39e-05
polygon 61 (hole)        3 -1.98390e-03     -2.54e-12
polygon 62 (hole)        4 -1.13774e-02     -1.46e-11
polygon 63              14  5.86546e+03      7.50e-06
polygon 64              95  5.96187e+04      7.62e-05
polygon 65 (hole)        4 -1.86410e-02     -2.38e-11
polygon 66 (hole)        3 -5.12482e-03     -6.55e-12
polygon 67 (hole)        3 -1.96410e-03     -2.51e-12
polygon 68 (hole)        3 -5.55856e-03     -7.11e-12
polygon 69             234  2.08755e+06      2.67e-03
polygon 70              10  4.90942e+02      6.28e-07
polygon 71             234  4.72886e+05      6.05e-04
polygon 72 (hole)       13 -3.91907e+02     -5.01e-07
polygon 73              15  4.03300e+04      5.16e-05
polygon 74             227  1.10308e+06      1.41e-03
polygon 75              10  6.60195e+03      8.44e-06
polygon 76              19  3.09221e+04      3.95e-05
polygon 77             145  9.61782e+05      1.23e-03
polygon 78              30  4.28933e+03      5.49e-06
polygon 79              37  1.29481e+04      1.66e-05
polygon 80               4  9.47108e+01      1.21e-07
enclosing rectangle: [2667.54, 56396.44] x [15748.72, 50256.33] units
                     (53730 x 34510 units)
Window area = 781945000 square units
Fraction of frame area: 0.422

As shown above, we can display the summary information of the owin object class.

8 Combining point events object and owin object

To combine point events object and owin object:

childcareSG_ppp = childcare_ppp[sg_owin]
plot(childcareSG_ppp)

9 Kernel Density Estimation of Spatial Point Event

In this section, we will show why we should re-scale to appropriate unit of measurement before performing KDE. 

kde_childcareSG_adaptive_m <- adaptive.density(
  childcareSG_ppp,
  method="kernel")

childcareSG_ppp.km <- rescale.ppp(childcareSG_ppp,
                                  1000,
                                  "km")

kde_childcareSG_adaptive_km <- adaptive.density(
  childcareSG_ppp.km,
  method="kernel")


par(mfrow=c(1,2))

plot(kde_childcareSG_adaptive_m)
plot(kde_childcareSG_adaptive_km)

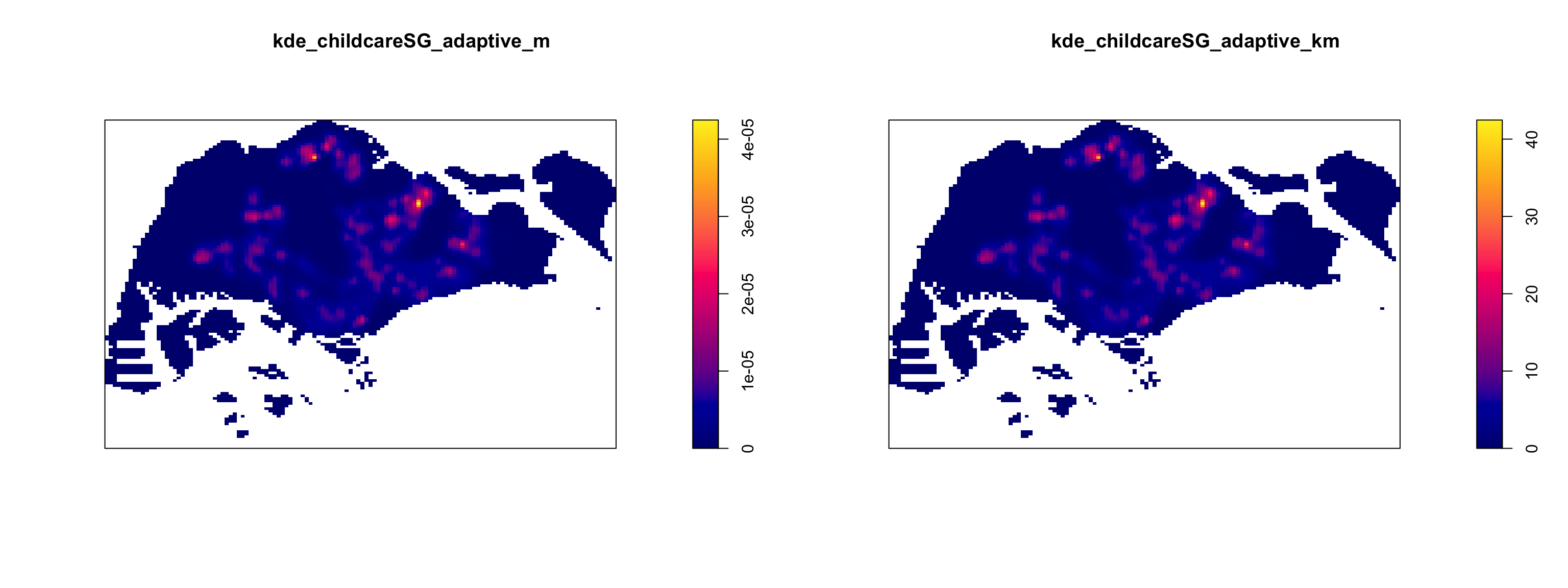
From the output above, we can notice that the plot on the right has a more interpretable scale range from 0-40km range as compared to the left plot where rescaling was not performed.

10 Kernel Density Estimation

There is 2 different ways to convert KDE output into grid object. spatstat.geom is preferred. 

gridded_kde_childcareSG_ad <- as(
  kde_childcareSG_adaptive_km,
  "SpatialGridDataFrame")
spplot(gridded_kde_childcareSG_ad)

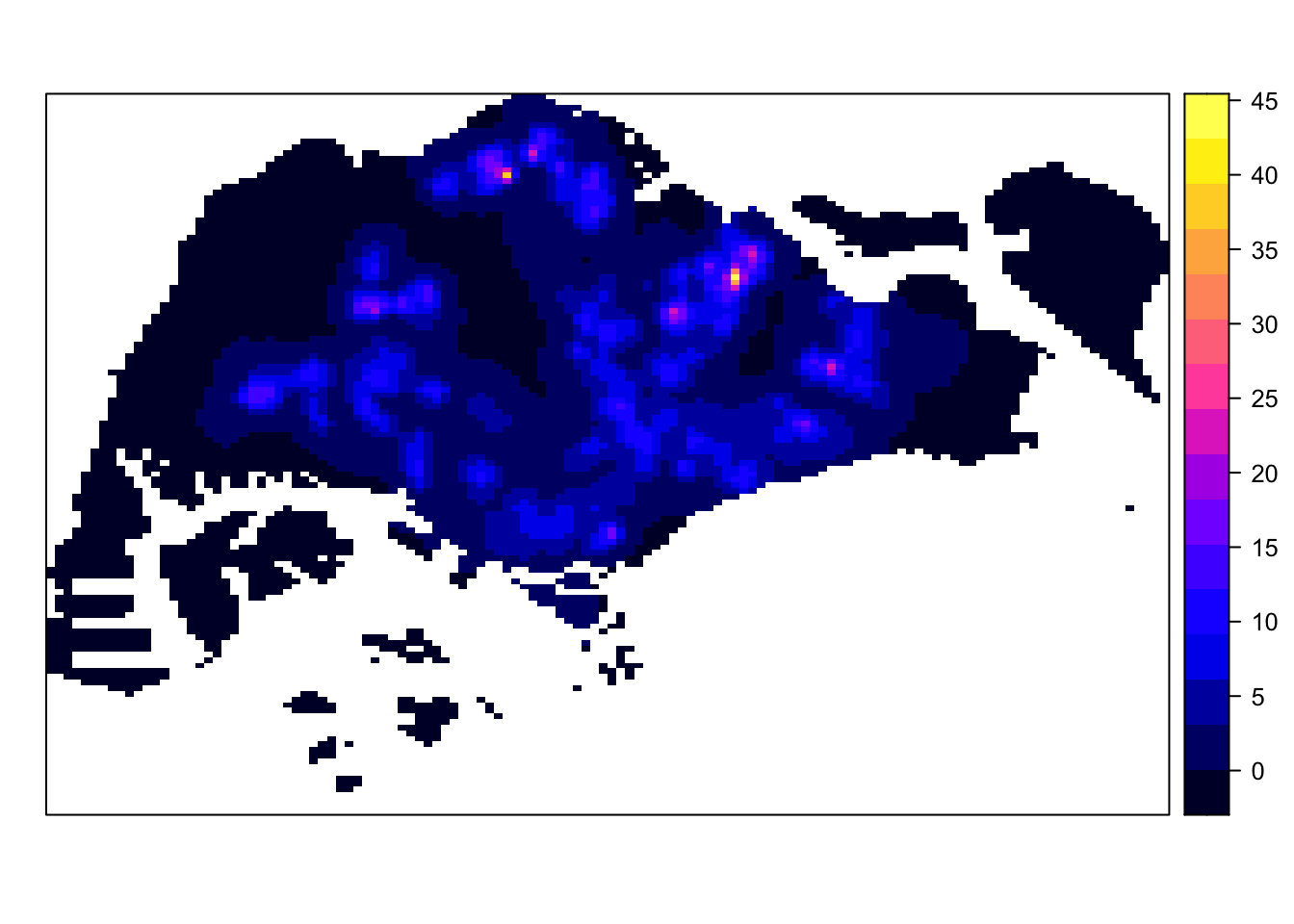
gridded_kde_childcareSG_ad <- maptools::as.SpatialGridDataFrame.im(
  kde_childcareSG_adaptive_km)
spplot(gridded_kde_childcareSG_ad)

11 Kernel Density Estimation

11.1 Visualising KDE using tmap

To visualize KDE in raster output using tmap:

tm_shape(kde_childcareSG_ad_raster) +
  tm_raster(palette = "viridis") +
  tm_layout(legend.position = c("right", "bottom"),
            frame = FALSE)

12 Extracting Study Area Using sf Objects

To extract and create an ppp object showing child care services and within Punggol Planning Area:

Tip

filter() of dplyr package should be used to extract the target planning areas. 

pg_owin <- mpsz_sf %>%
  filter(PLN_AREA_N == "PUNGGOL") %>%
  as.owin()

childcare_pg = childcare_ppp[pg_owin]

plot(childcare_pg)

13 Monte Carlo Simulation

Tip

In order to ensure reproducibility, it is important to include the code block below before using spatstat functions involve Monte Carlo simulation 

set.seed(1234)

14 Edge Correction Methods of spatstat

In spatstat, edge correction methods are used to handle biases that arise when estimating spatial statistics near the boundaries of a study region. These corrections are essential for ensuring accurate estimates in spatial point pattern analysis, especially for summary statistics like the K-function, L-function, pair correlation function, etc.

Method Description
none No edge correction is applied. Assumes no bias at the edges, which may lead to underestimation of statistics near the boundaries.
isotropic Corrects for edge effects by assuming the point pattern is isotropic (uniform in all directions) and compensates for missing neighbors outside the boundary.
translate (Translation Correction) Uses translation correction by translating the observation window so every point lies entirely within it, then averaging statistics over all translations.
Ripley (Ripley’s Correction) Similar to isotropic correction, but specifically tailored for Ripley’s K-function and related functions. Adjusts the expected number of neighbors near edges based on the window’s shape and size.
border Border correction reduces bias by only considering points far enough from the boundary so that their neighborhood is fully contained within the window, minimizing edge effects.

15 Geospatial Analytics for Social Good: Thailand Road Accident Case Study

This section is in preparation of Take-home Exercise 1: Geospatial Analytics for Public Good

15.1 Background

For an overview of the road traffic accidents in Thailand, you may refer to:

15.2 The Study Area

The study area is Bangkok Metropolitan Region.

Note

The projected coordinate system of Thailand is WGS 84 / UTM zone 47N and the EPSG code is 32647.

15.3 The Data

For the purpose of this exercise, three basic data sets are needed, they are:

15.3.1 Traffic Accident Data 

rdacc_sf <- read_csv("data/geospatial/thai_road_accident_2019_2022.csv") %>%
  filter(!is.na(longitude) & longitude != "",
         !is.na(latitude) & latitude != "") %>%
  st_as_sf(coords = c(
    "longitude", "latitude"),
    crs=4326) %>%
  st_transform(crs = 32647)
plot(rdacc_sf)

15.3.2 Administrative Boundary 

# country
adminboundary0 <- st_read(dsn = "data/geospatial",
                layer = "tha_admbnda_adm0_rtsd_20220121")
Reading layer `tha_admbnda_adm0_rtsd_20220121' from data source
  `/Users/walter/code/isss626/isss626-gaa/In-class_Ex/In-class_Ex02/data/geospatial'
  using driver `ESRI Shapefile'
Simple feature collection with 1 feature and 13 fields
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: 97.34336 ymin: 5.613038 xmax: 105.637 ymax: 20.46507
Geodetic CRS:  WGS 84
# # province
# adminboundary1 <- st_read(dsn = "data/geospatial",
#                 layer = "tha_admbnda_adm1_rtsd_20220121")

# # district
# adminboundary2 <- st_read(dsn = "data/geospatial",
#                 layer = "tha_admbnda_adm2_rtsd_20220121")

# # sub-district
# adminboundary3 <- st_read(dsn = "data/geospatial",
#                 layer = "tha_admbnda_adm3_rtsd_20220121")
plot(adminboundary0, max.plot=1)

# plot(adminboundary1)
# plot(adminboundary2)
# plot(adminboundary3)

15.3.3 Thai Roads 

roads <- st_read(dsn = "data/geospatial",
                layer = "hotosm_tha_roads_lines_shp")
Reading layer `hotosm_tha_roads_lines_shp' from data source
  `/Users/walter/code/isss626/isss626-gaa/In-class_Ex/In-class_Ex02/data/geospatial'
  using driver `ESRI Shapefile'
Simple feature collection with 2792590 features and 14 fields
Geometry type: MULTILINESTRING
Dimension:     XY
Bounding box:  xmin: 97.34457 ymin: 5.643645 xmax: 105.6528 ymax: 20.47168
CRS:           NA